37 KiB
Executable File
| author | title | |
|---|---|---|
|
Física Nuclear I |
Introducción
Hasta este punto hemos hablado de la dispersión de Rutherford, de las partículas y de los experimnentos para detectarlas, como les mencioné ese no es exactamente el órden histórico.
Los experimentos de Rutherford, Geiger y Marsden mostraron que los átomos tienen un núcleo positivo, pero estudios posteriores para obtener más detalles al respecto mostraron que no sólo hay interacción coulombiana, hay otras fuerzas dentro, y que además de protones en el núcleo hay neutrones.
En 1932 Chadwick, seguramente acompañado de un equipo más amplio de investigadores, descubrió el neutrón. A nivel de partículas ya estudiamos los dos constituyentes nucleares, ahora veamos como se comporta este objeto compuesto llamado núcleo.
Propiedades del núcleo
Etiquetado
Un núcleo lo nombramos igual que al elemento que pertenece, puede se H,
He, C, Fe, U, etc., con ligeras diferencias. Tenemos un núcleo X,
además de ser identificado por el nombre, como redundancia es
identificado por su Z. Lo que define a un núcleo justo es eso, su
número atómico. Además agregamos la cantidad de nucleones que posee,
nótese que A no define que núcleo es, veamos porque.
Tenemos nuestro núcleo {}^AX^Z, con Z protones y N-Z neutrones, de
aquí podemos identificarlo como respecto a otro núecleo
{}^{A'}{X'}^{Z'}
-
Isótopo: núcleos con el mismo número de protones pero distinto número de nucleones,
{}^AX^Zy{}^{A'}{X}^{Z}son isótopos del núcleoX. -
Isóbaros: núcleos con el mismo número de nucleones pero distinto número de protones,
{}^AX^Zy{}^{A}{X'}^{Z'}son isóbaros. -
Isómeros o resonancias: núcleos exitados a niveles más altos de energía.
Masa del núcleo
Ya vimos un poco de la convención sobre como se etiqueta un núcleo y algunos de los términos a usar, ahora vemos las características del mismo.
Si tenemos un núcleo {}^AX^Z y queremos obtener su masa uno pensaría
que es tan fácil como sumar la masa de los protones y neutrones que
contiene:
M({}^AX^Z) = M(A,Z) = Zm_p + (A-Z)m_nPero experimentalemente se encuentra que la masa del núcleo es menor a la suma de las masas de sus constituyentes, es decir
M(A,Z)< Zm_p + (A-Z)m_nPor ello es que los núcleones están confinados en el núcleo, es un estado energéticamente más favorable. Definimos el defecto de masa como
\Delta M(A,Z) = M(A,Z) - Zm_p - (A-Z)m_n,que es un valor negativo, y es proporcional a la energía de enlace nuclear, de la forma
B.E. = \Delta M(A,Z)c^2De esta forma -B.E. es la cantidad de energía necesaria para liberar a
todos los nucleones de su estado ligado como núcleo, Si \Delta M(A,Z)
es negativa, y por ende B.E., el núcleo es ligado, mientras más
negativo sea el valor más ligado es.
La energía promedio para liberar un nucleón se da por la razón
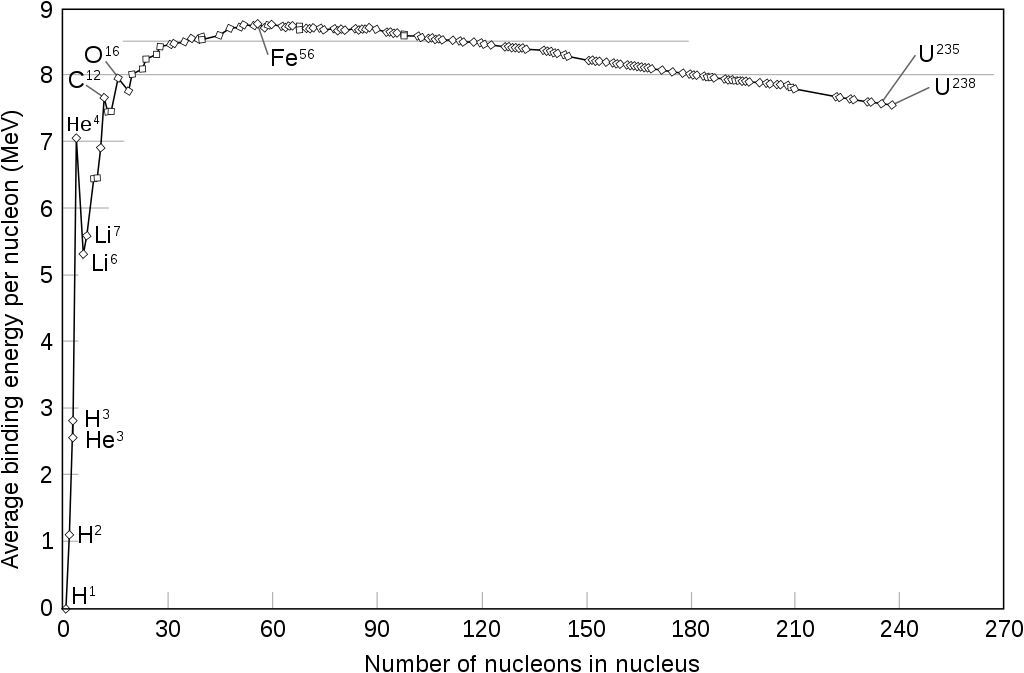
\frac{B}{A} = \frac{-B.E.}{A} = \frac{-\Delta M(A,Z)c^2}{A}Este valor es útil pues pensaríamos que la energía de enlace por nucleón
B/A, si todo se comportara bien, sería una constante, mas su
comportamiento nos da más características de esta energía, como se puede
ver en la figura 1{reference-type="ref"
reference="fig:binding"}. Para núcleos ligeros B/A oscila un poco,
aumenta rápidamente y se satura, alcanzando un pico alrededor de los
9\ MeV por nucleón, que en el eje de las X corresponde a un
A = 60. Para A mayor B/A decae lentamente. 8\ MeV es un valor
promedio para estos núcleos restantes, nos sirve para ver que esperamos
obtener.
 {#fig:binding
width="0.7\linewidth"}
{#fig:binding
width="0.7\linewidth"}
¿Cómo se calcula la masa de un núcleo a partir de datos que conocemos? Para obtener la masa la primera opción es buscar la tabla de todos los isótopos, eso es complicado y muy extenso, que puede cambiar dependiendo del experimento. Lo siguiente sería tener el defecto de masa o la energía de enlace. Usaremos esta opción pero con unos valores reducidos llamados excesos de masa
\delta (A,Z) = [M(Z,A)[uma] - A]keV/c^2\ c^2M(Z,A) es el valor experimental, pero lo empaquetamos en un nuevo
valor llamado exceso de masa, si queremos obtener la masa experimental
de un núcleo basta con tener su exceso de masa y el número de nucleones.
Para obtener la energía de enlace a partir de los exceso de masa
\begin{aligned}
B.E. =& M(A,Z) - Zm_p - (A-Z)m_n \\
=& (\delta(A,Z) + A) - Z(\delta(1,1) + 1) - (A-Z)(\delta(1,0)+1) \\
=& \delta(A,Z) + A -Z\delta(1,1) - Z - A\delta(1,0) - A + Z\delta(1,0) +Z \\
=& \delta(A,Z) -Z\delta(1,1) - (A-Z)\delta(1,0)\end{aligned}$$
Veamos un ejemplo. Tenemos el oxígeno estable ${}^{18}O^8$, el exceso de
masa del núcleo es (revisando
<https://www-nds.iaea.org/amdc/ame2016/mass16.txt>)
$\delta(16,8) = -4737.00135\ keV$, siempre usaremos la del protón
$\delta(1,1) = 7288.97061 keV$ y la del neutrón
$\delta(1,0) = 8071.31713\ keV$, ahora calculemos la energía de enlace
del núcleo:
$$\begin{aligned}
B.E. =& \delta(16,8) -8\delta(1,1) - 8\delta(1,0) \\
=& -4737.0013keV - 8(7288.9706keV) - 8(8071.3171keV) \\
=& -91619.3032 keV\end{aligned}$$
Tamaños del núcleo {#tamaños-del-núcleo .unnumbered}
------------------
El tamaño en un sistema cuántico se define como el valor promedio del
operador de coordenada en un estado propio, en un átomo este valor
promedio de coordenada se toma en el electrón más externo, pero como en
el núcleo es difícil tener una expresión exacta de las fuerzas que
actúan se harán otras aproximaciones.
Pensemos en la dispersión de Rutherford, si el impacto de la partícula
con el núcleo es frontal, la partícula será retro dispersada, la
distancia de máxima aproximación se da como:
$$r_0^{min} = \frac{ZZ'e^2}{E}$$
que se obtiene sacando el mínimo en la ecuación del campo eléctrico.
Esta distancia de mínima aproximación es frontal, la partícula (sea una
$\alpha$) rebota y lo más cerca que está del núcleo es la primera
aproximación al tamaños del núcleo. Es una mala aproximación pues está
una barrera coulombiana antes de que el $\alpha$ pueda acercarse más al
núcleo. Por ejemplo, para el oro y la plata esta aproximación da
$R_{Au} \lesssim 3.2\times 10^{-12}cm.$ y
$R_{Ag} \lesssim 2\times 10^{-12} cm$, que no son muy buenas
aproximaciones (más adelante probaremos mejores).
Si aumentamos la energía de la $\alpha$ para pasar la barrera
coulombiana llegamos al extremo de que $r_0^{min} \rightarrow 0$. Una
mejor manera de investigar el núcleo a altas energía es usar un
electrón, así evitamos la acción de la interacción nuclear fuerte, con
energía suficiente puede deducir la distribución de cargas dentro del
núcleo, el radio de esta distribución es una mejor aproximación al radio
nuclear. A altas energía el momento magnético del electrón también
interfiere en la interacción. Motts amplió la teoría de Rutherford para
incluir la cuántica y estudios sistemáticos de electrones relativistas
chocando con el núcleo se deben a Robert Hofstadter.
Para una distribución de cargas $\rho(\overrightarrow{r})$ podemos
definir el factor de forma de la distribución a partir de la
transformada de Fourier:
$$F(\overrightarrow{q}) = \int_\text{todo el espacio} d^3 r \rho (\overrightarrow{r}) e^{\frac{i}{\hbar}\overrightarrow{q}\cdot \overrightarrow{r}}$$
Este factor de foma altera la sección eficaz diferencial de las
colisiones elásticas de electrones desde centros puntuales:
$$\frac{d\sigma}{dq^2} = |F(\overrightarrow{q})|^2 \left( \frac{d\sigma}{dq^2} \right)_{Mott}$$
que a su vez
$$\left( \frac{d\sigma}{d\Omega} \right)_{Mott} = 4cos^2\frac{\theta}{2} \left( \frac{d\sigma}{d\Omega} \right)_{Rutherford}$$
Que le agrega la parte cuántica a la sección eficaz de Rutherford.
La siguiente aproximación se puede hacer con hadrones de altas energías,
como piones y protones, rompen la barrera coulombiana pero de manera
análoga a los electrones ahora pueden deducir la forma del núcleo pero
sólo tomando en cuenta la fuerza nuclear fuerte.
Todas estas aproximaciones nos dan un valor para el radio del núcleo:
$$\begin{aligned}
R &= r_0 A^{\frac{1}{3}} \\
&\approx 1.2\times 10^{-13} A^{\frac{1}{3}}cm.= 1.2A^{\frac{1}{3}}fm. \end{aligned}$$
Por ejemplo, para el ${}^{197}Au^{79}$, su radio sería
$R\approx 1.2 (197)^{\frac{1}{3}}fm = 6.9824 fm$, un órden de magnitud
menor que la aproximación anterior.
Espines nucleares y momentos dipolares {#espines-nucleares-y-momentos-dipolares .unnumbered}
--------------------------------------
Rememorando la parte de espín en partículas elementales, sabemos que los
protones y neutrones tienen espín $\hbar/2$ y un momento angular
(entero) asociado. La suma que ya conocemos de momento angular define el
momento angular del núcleo, pero hay detalles. Por el momento la parte
fenomenológica nos dice que:
- Núcleos con número atómico par tienen espín nuclear entero
- Núcleos con número atómico impar tienen espín nuclear semi-entero
- Núcleos con número par de protones y número par de protones
(par-par) tienen espín nuclear cero
- Núcleos muy grandes tienen espín nuclear muy pequeño en su estado
base
- Hace pensar qu los nucleones dentro del núcleo están fuertemente
apareados
Por otro lado, el momento dipolar magnético para una partícula cargada
está dado por
$$\overrightarrow{\mu} = g\frac{e}{2mc}\overrightarrow{S},$$
con $e$ la carga, $m$ la masa y $\overrightarrow{S}$ el espín de la
partícula cargada; $g$ es el factor de Landé y es diferente para
distintas partículas. Para los nucleones definimos el magnetón nuclear
(similar al magnetón de Bohr para electrones):
$$\mu_N = \frac{e\hbar}{2m_pc},$$
y a partir de él se define el momento magnético del protón y en neutrón
$$\mu_p \approx 2.79\mu_N, \ \mu_n \approx -1.91\mu_N.$$
Son momentos magnéticos bastante grandes y anómalos, sobre todo para el
neutrón (¡que es neutro!), lo que hizo sospechar que eran partículas
compuestas.
Estabilidad de los núcleos {#estabilidad-de-los-núcleos .unnumbered}
--------------------------
Ya les he contado, ya saben un poco de su experiencia, que hay núcleos
estables y otros que decaen fácilmente en otros núcleos. Si observamos
lo que los experimentos y observaciones nos dicen, para $A\lesssim 40$
el número de protones y neutrones se mantiene igual (para los núcleos
estables, recuerden), es decir $N=Z=A/2$, pero para núcleos más pesados
$N\approx 1.7Z$, en promedio hay $1.7$ veces más neutrones que protones,
casi el doble pero no llega a tanto. El exceso e neutrones evita que la
inestabilidad por carga aumente. Una ionterpretación como islas puede
verse en al figura [2](#fig:islas){reference-type="ref"
reference="fig:islas"}.
Las observaciones además nos dicen que los núcleos más estables más
abundantes suelen ser par-par.
------- ------- ----------------------------
N Z Número de núcleos estables
Par Par $156$
Par Impar $48$
Impar Par $50$
Impar Impar $5$
------- ------- ----------------------------

by [InvaderXan](https://commons.wikimedia.org/wiki/User:InvaderXan) is
licensed under [CC BY-SA
3.0.](https://creativecommons.org/licenses/by-sa/3.0/?ref=openverse)
](islase.jpg){#fig:islas width="0.7\\linewidth"}
Inestabilidad del núcleo {#inestabilidad-del-núcleo .unnumbered}
------------------------
La radiactividad fue descubierta por accidente en 1896 en el trabajo de
Henry Becquerel, observando un efecto de radiactividad naturar en las
sales de uranio, un núcleo bastante pesado.
Ya hablamos de los tres tipos de radiación
- $\alpha$, núcelos de ${}^4He^2$
- $\beta$, electrones
- $\gamma$, fotones de muy alta energía
En esos primeros estudios (un poco después de Becquerel) se descubrió
que para detener la radiación $\beta$ se requiere una pared de plomo,
$3mm.$ para las energías de esta radiación de forma natural, una hoja de
papel para partículas $\alpha$, y para los $\gamma$ se requieren varios
centímetros de plomo para poder detenerlos (absorberlos).
Fuerza nuclear {#fuerza-nuclear .unnumbered}
--------------
Otro tópico que ya hemos tratado, sabemos que es de corto alcance, actúa
sobre los hadrones y por ello podemos tener un núcleo formado por protón
y neutrón (el deuterio, que a pesar de no ser estable sí existe por un
momento).
El hecho de que la energía de enlace por núcleon tienda a una constante
es muestra del corto alcance de esta fuerza, se satura. Esta fuerza a su
vez de ser atractiva tiene un núcleo repulsivo (lo que evita que colapse
el núcleo), por ello podemos pensar esta fuerza como un pozo de
potencial (como el de la figura [3](#fig:pozo){reference-type="ref"
reference="fig:pozo"}). Por ser un pozo de potencial de inmediato
sabemos que hay estados ligados cuantizados y que de ahí deriva un
modelo que se parcerá mucho al modelo de nivles atómicos, pero de eso ya
hablaremos en la próxima sección.
{#fig:pozo width="0.6\\linewidth"}
Modelos nucleares {#modelos-nucleares .unnumbered}
=================
Los modelos que trataremos son fenomenológicos, por las complicadas
características de la fuerza nuclear fue necesario tomar ese camino. Ya
en la sección anterior hablamos de algunas de las características que
definen a estos modelos.
Modelo de la gota {#modelo-de-la-gota .unnumbered}
-----------------
Los experimentos muestran que el núcleo parece tener una estructura
esférica, con un radio, eso es lo primero que nos hace pensar en una
gota, además de la incompresibilidad del fluido y su estructura hay
algunas características extras que asemejan a un fluido. Pero en este
modelo las características particulares de los nucleones son desechadas.
La gota está formada por nucleones como si fueran moléculas, los del
interior están saturados, es dificil desprenderlos, y los de la orilla
no están saturados, se separan más fácil, lo que asemeja a la tension
superficial.
A partir de estas consideraciones podemos ir aproximando la energía de
ligadura
$$B.E. = -a_1 A + a_2 A^{\frac{2}{3}}$$
El primer término se refiere a la energía en el volumen, saturada, el
segundo a la tensión superficial. Núcleos más ligeros tienen más
nucelones en la superficie que en el volumen. Explica un poco el rápido
crecimiento al inicio de la gráfica $B/A$.
Centrándonos de nuevo en esa gráfica $B/E$, vemos que a altas energías
el valor decrece, lentamente, pero decrece. Eso puede deberse a la
repulsión coulombiana entre protones
$$B.E. = -a_1 A + a_2 A^{\frac{2}{3}} + a_3 \frac{Z^2}{A^{\frac{1}{3}}}$$
Todas estas son consideraciones clásicas, pero hace falta agregar la
estabilidad del núcleo. Recordemos que lo más estable para núcleos
ligeros es $N=Z$, los núcleos par-par son más estables sin importar si
son ligeros o pesados, los núcleos par-impar ya no son tan estables, y
los impar-impar son los menos estables. Requerimos un término que
responda a ello (efectos muy probablemente cuánticos)
$$B.E. = -a_1 A + a_2 A^{\frac{2}{3}} + a_3 \frac{Z^2}{A^{\frac{1}{3}}} + a_4\frac{(N-Z)^2}{A} \pm a_5A^{-\frac{3}{4}},$$
se asume que los coeficientes $a_1$, $a_2$, $a_3$, $a_4$ y $a_5$ son
positivos, de esta forma los signos también nos dan información de la
fenomenología (cómo aportan a la energía de ligadura y por lo tanto a la
estabilidad del núcleo). El cuarto término nos asegura que si $N\neq Z$
la energía de enlace es mayor, por ende el núcleo es más inestable. Para
núcleos ligeros el tercer término no afecta tanto, y el cuarto no aporta
nada a disminuir la energía de enlace con $N=Z$. En el quinto término el
signo positivo se elige para núcleos impar-impar, negativo para los
núclos par-par y $a_5=0$ para núclos impar-par.
Los valores de los coeficientes se obtinen de ajustar el modelo a los
datos empíricos
$$\begin{aligned}
a_1\approx 15.5\ MeV, \ \ a_2 &\approx 16.8\ MeV, \ \ a_3 \approx 0.72\ MeV, \\
a_4 &\approx 23.3\ MeV, \ \ a_5 \approx 34\ MeV.\end{aligned}$$
Se puede sustituir en la fórmula para masas respecto a la energía de
ligadura
$$M(A,Z) = Zm_p + (A-Z)m_n + \frac{B.E.}{c^2}$$
y obtener una relación de la fórmula semi empírica con la masa
$$\begin{aligned}
M(A,Z) =& Zm_p + (A-Z)m_n -\frac{a_1}{c^2}A \\
&+ \frac{a_2}{c^2} + \frac{a_3}{c^2} \frac{Z^2}{A^{\frac{1}{3}}} + \frac{a_4}{c^2}\frac{(N-Z)^2}{A} \pm \frac{a_5}{c^2}A^{-\frac{3}{4}}\end{aligned}$$
ES la fórmula semi-empírica de Bethe-Weizsäcker para masas nucleares,
puede dar información sobre estabilidad de núcleos aún no conocidos (de
cualquier $A$ y $Z$), y es de mucha ayuda para entender la fisión
nuclear.
Modelo de gas de Fermi {#modelo-de-gas-de-fermi .unnumbered}
----------------------
Si queremos agregar las cuestiones cuánticas que conocemos (sobre todo
las relacionadas con el espín) el siguiente modelo es el de gas de
Fermi, el primero en implementar la parte cuántica. Considera al núcleo
un gas de protones y neutrones confinado en una región pequeña el
espacio, el núcleo. De manera análoga a los electrones en el átomo, los
nucleones llenarán niveles de energía cuantizados. Esos niveles serán
distintos para protones y para neutrones, el primero debe incluir la
repulsión coulombiana, el ancho estará dado por el radio nuclear y la
profundidad puede ajustarse de acuerdo a la energía de enlace.
El pozo se va llenando (vamos acomodando protones o neutrones) de abajo
hacia arriba, los niveles más bajos son los más estables, el último
nivel completamente lleno se le llama nivel de Fermi y se denota por la
energía $E_F$. Si más allá de ese nivel ya no hay nucleones, la energía
de enlace es $E_F$, si hay uno fuera de capa cerrada, ese mismo definen
la energía de enlace del último nucleón.
La profundidad de los pozos para protones y neutrones son distintas, de
no ser así los núcleos pesados tendrían niveles de energía por arriba
para neutrones, haciendo sólo la parte neutra más inestable con una
energía de enlace distinta, pero eso no se observa en el experimento. Un
esquema de los pozos se puede ver en la figura
[4](#fig:fermi){reference-type="ref" reference="fig:fermi"}.
,
con licencia
[CC-BY-NC-SA](https://creativecommons.org/licenses/by-nc-sa/2.0/)](fermi.jpg){#fig:fermi
width="0.7\\linewidth"}
Hagamos un cálculo sencillo de la energía de Fermi. La relación del
momento y la energía de Fermi
$$E_F = \frac{p_F^2}{2m}$$
Ignorando fermiones más allá de este nivel tenemos el volumen de estados
en el espacio de momentos
$$V_{p_F} = \frac{4\pi}{3} p_F^3$$
Si $V$ es el volumen físico del núcleo entonces el volumen total de
estados, o *espacio fase* está dado por
$$\begin{aligned}
V_{TOT} =& V\times V_{p_F} = \frac{4\pi}{3}r_0^3A \times \frac{4\pi}{3}p_F^3 \\
=& \left( \frac{4\pi}{3} \right)^2 A (r_0 p_F)^3 \end{aligned}$$
Que es proporcional a la cantidad total de estados cuánticos del sistema
(están bien ordenados y cubren el volumen). Recordando la incertidumbre
de Heisenberg
$$\Delta x \Delta p \geq \frac{\hbar}{2}$$
 con licencia
[CC-BY-SA](https://creativecommons.org/licenses/by-sa/3.0/deed.en)](fase.jpg){#fig:fase
width="0.5\\linewidth"}
Que a su vez nos dice el mínimo volumen que se le puede asociar a un
estado físico en el espacio fase
$$V_{estado} = (2\pi \hbar)^3 = h^3$$
Entonces el número de fermiones que pueden llenar los estados
$$n_F = 2\frac{V_{TOT}}{(2\pi\hbar)^3} = \frac{2}{(2\pi\hbar)^3} \left( \frac{4\pi}{3} \right)^2 A (r_0 p_F)^3 = \frac{4}{9\pi}A \left( \frac{r_0 p_F}{\hbar} \right)^3,$$
el 2 se debe al principio de exclusión de Pauli, cada estado puede estar
ocupado por dos fermiones de espín contrario.
Supongamos que $N=Z$ (para núcleos ligeros es completamente válido, para
más pesados es una aproximación) y además suponemos que el estado de
Fermi está lleno
$$\begin{aligned}
N=Z=\frac{A}{2} =& \frac{4}{9\pi}A \left( \frac{r_0 p_F}{\hbar} \right)^3 \\
\text{despejando } p_F =& \frac{\hbar}{r_0} \left( \frac{9\pi}{8} \right)^{\frac{1}{3}}.\end{aligned}$$
Ese momento de Fermi depende de puras constantes, es independiente del
número de nucleones, ahora
$$\begin{aligned}
E_F = \frac{p_F^2}{2m} = \frac{1}{2m} \left( \frac{\hbar}{r_0} \right)^2 \left( \frac{9\pi}{8} \right)^{\frac{2}{3}}\approx 33\ MeV\end{aligned}$$
Si tomamos $B/A\approx 8\ MeV$ será la profundidad a la que ajustaremos
nuestro pozo para tomar en cuenta la energía de enlace, entonces
$$V_0 = E_F + \frac{B}{A} \approx 40\ MeV$$
Valor que se ajusta con lo obtenido por otros métodos. Este modelo es
útil al hablar de estados excitados del núcleo y justifica el termino
$a_4$ de la fórmula semi-empírica.
Modelo de capas {#modelo-de-capas .unnumbered}
---------------
El modelo de capas es un modelo de partícula independiente, a diferencia
de gas de Fermi ahora tratamos de identificar el potencial. Para ello
recordemos un poco el modelo de capas atómico.
Las energías están cuantificadas, cada nivel energético es etiquetado
por el número principal cuántico $n$ con valores enteros. Para cada
valor de $n$ hay estados degenerados en energía con momento angular
orbital $\ell$, también con valores enteros desde $0$ hasta $n-1$.
Para cada número $\ell$ a su vez hay $2\ell + 1$ subestados que
corresponden a las distintas proyecciones del momento angular orbital.
Debido a la simetría rotacional todos los estados de proyección de
momento angular están degenerados en energía. A su vez las partículas
tienen un momento angular intrínseco $s$ entero o semi-entero que tiene
$2s+1$ proyecciones.
Así cada estado de un electrón en el átomo está dado por el conjunto de
números cuánticos ($n$, $\ell$, $m_{\ell}$, $m_s$). En total de estados
degenerados se tienen:
$$\begin{aligned}
n_d &= 2\sum_{\ell=0}^{n-1} (2\ell + 1) \\
&= 2 \left( 2\sum_{\ell=0}^{n-1} \ell + \sum_{\ell=0}^{n-1} 1 \right) \\
&= 2 \left( 2 \times \frac{1}{2} n(n-1) + n \right) \\
&= 2(n^2-n+n) = 2n^2\end{aligned}$$
Si hay una dirección preferida del espacio, por ejemplo cuando se pone
un campo magnético a lo largo del eje $z$, se rompe la degeneración, y
entonces para cada combinación de números cuánticos tenemos estados
distintos de energía, es decir, la energía depende también de $m_{\ell}$
y $m_s$.
A nivel de potencial este rompimiento de la degeneración sucede al
agregar al término del potencial coulombiano el producto vectorial
$-\overrightarrow{\mu}\cdot \overrightarrow{B}$.
Interacciones debidas al acoplamiento espín-orbita (en este caso el
campo magnético que afecta al espín del electrón es el derivado del
momento angular órbital del núcleo) puede romper otras degeneraciones,
derivando en la estructura fina que es estudiada como tema muy
particular de la física atómica, rara vez vista en un curso básico. Pero
estos acoplamientos también son útiles para describir características
del núcleo.
Podemos ir viendo el sistema cuántico por niveles de degeneración, sin
tomar en cuenta estructura fina el átomo tiene $n$ niveles de energía
donde acomodar electrones, cada uno de estos niveles de energía tienen
subcapas etiquetadas por el valor de $\ell$. Al introducir la
interacción coulombiana electrón-electrón cada nivel $n$ se divide en
varios niveles, de acuerdo al valor de $\ell$. Si $\ell$ es muy grande
el átomo se vuelve menos esférico y hace al átomo menos estable. Si
todas las capas y subcapas están llenas sabemos que la suma de los
números cuánticos $m_{\ell}$ y $m_s$ son cero, es decir que hay un
apareamiento muy fuerte para capas cerradas, en esos casos
$\overrightarrow{L}=0=\overrightarrow{S}$ y por tanto
$\overrightarrow{J} = \overrightarrow{L} + \overrightarrow{S}=0$.
¿Qué átomos terminan en capa cerrada? Los gases nobles, que son inertes.
Tienen números atómicos: $Z=2,10, 18,36,54,$ que son los números mágicos
de física atómica.
En física nuclear también existe evidencia de números mágicos nucleares,
para este número de protones o neutrones el núcleo es más estable, estos
valores son
$$\begin{aligned}
N =& 2,8,20,28,50,82,126 \\
Z =& 2,8,20,28,50,82.\end{aligned}$$
Los núcleos con alguno de esos valores en $Z$ o $N$ son muy estables y
se llaman núclos mágicos, los que tienen $N$ y $Z$ con valores mágicos,
ambos, son núcleos doblemente mágicos, aún más estables (${}^4He^2$,
${}^{16}O^8$, ${}^{208}Pb^{82}$).
Además los núcleos mágicos tienen más isótopos e isótonos (mismo número
de neutrones, distinto de protones) estables que sus vecinos no mágicos
($Sn$, con $Z=50$, tiene diez isótopos estables, mientras que $In$ con
$Z=49$ y $Sb$ con $Z=51$ sólo tienen dos isótopos estables), esto, los
números mágicos, el hecho de que para núcleos mágicos el momento
cuadrupolar se haga cero, nos hace pensar de una estructura de capas en
el núcleo.
Listo, hagamos un modelo de capas como en el átomo. Pero no, tenemos
problemas
- En el núcleo a diferencia del átomo no tenemos un núcleo central que
provee la energía de enlace
- Debemos considerar entonces un potencial central efectivo
- La fuerza nuclear no es tan bien entendida como la fuerza
coulombiana del átomo.
A pesar de estos problemas consideremos que hay un potencial central, la
ecuación de Schrödinger para eso:
$$\begin{aligned}
\left( -\frac{\hbar^2}{2m}\overrightarrow{\nabla}^2 + V(\overrightarrow{r}) \right) \psi(\overrightarrow{r}) =& E \psi(\overrightarrow{r}) \\
\text{ó } \left( \overrightarrow{\nabla}^2 + \frac{2m}{\hbar^2}(E-V(\overrightarrow{r})) \right) \psi(\overrightarrow{r}) =& 0, \end{aligned}$$
$E$ es el valor propio de energía, y dado que el potencial se considera
con simetría esférica, los estados propios de energía también son
estados propios del operador de momento angular (el operador de momento
angular conmuta con el Hamiltoniano, hay simetría esférica). Usemos
coordenadas esféricas y etiquetemos los estados propios de energía por
los números cuánticos de momento angular
$$\overrightarrow{\nabla}^2 = \frac{1}{r^2}\frac{\partial}{\partial r}r^2\frac{\partial}{\partial r} - \frac{1}{\hbar^2 r^2} \overrightarrow{L}^2,$$
para $\overrightarrow{L}^2$ con estados propios los armónicos esféricos
y sus valores propios $\hbar^2 \ell (\ell + 1)$. Podemos dividir la
ecuación de Schrödinger en su parte radial y la parte esférica, ya saben
como van las funciones para la parte radial y el número cuántico
asociado.
Pero para sacar más información debemos definir un potencial, dos casos
populares es el pozo infinito y el oscilador armónico (es un potencial
central). Ambos casos no son realistas pues no toman en cuenta la
posibilidad del tunelaje cuántico (cómo si sucedería en un pozo finito,
pero este sólo da soluciones numéricas que no nos dicen mucho de las
características del núcleo), pero para un estudio cualitativo sirven muy
bien.
### Pozo infinito de potencial {#pozo-infinito-de-potencial .unnumbered}
Definimos el potencial como
$$V(\overrightarrow{r})=\begin{cases}
\infty \quad &\text{si } r\geq R \\
0 \quad &\text{de otra forma,} \\
\end{cases}$$
con $R$ el radio nuclear. La ecuación radial para $0\leq r\leq R$ toma
la forma
$$\left( \frac{d^2}{dr^2} + \frac{2m}{\hbar^2} \left( E_{n\ell} - \frac{\hbar \ell(\ell + 1)}{2mr^2} \right) \right) u_{n\ell}(r) = 0$$
con soluciones regulares en el origen dadas por las funciones
oscilatorias Bessel esféricas $u_{n\ell}(r) = j_{\ell}(k_{n\ell}r)$, con
$$k_{n\ell} = \sqrt{\frac{2mE_{n\ell}}{\hbar^2}}.$$
Como el pozo es infinito los nucloenes no pueden escapar, la función
radial debe hacerse cero en las fronteras
$$u_{n\ell}(R) = j_{\ell}(k_{n\ell}R) = 0, \ \ \ell= 0,1,2,3,...\ y\ n=1,2,3,...\text{ para cualquier } \ell$$
donde las funciones Bessel esféricas tienen varios ceros. La única
degeneración aquí correspone a las proyecciones $m_{\ell}$, por ello
cada nivel puede llenarse con $2(2\ell + 1)$ protones o neutrones (por
el espín tenemos el doble de capacidad). De esta forma las capas
cerradas suceden, para $n=1$,
$$\mathbf{2}, 2+6=\mathbf{8}, 8+10=\mathbf{18}, 18+14=\mathbf{32}, 32+18=\mathbf{50},...$$
Y casi lo logramos, pero fallamos en obtener el $20$ y el $28$, y les
adelanto que ni el $82$ ni $126$. Aquí tomamos $n=1$, para otro valor de
$n$ se obtineen otros valores, pero no mejor. No es que hayamos hecho
todo esto en vano, sino que nos da una idea de como aproximarnos, pero
en definitiva este potencial no reproduce los números.
### Oscilador armónico {#oscilador-armónico .unnumbered}
La ecuación radial de un oscilador armónico en tres dimensiones
$$V(r) = \frac{1}{2} m\omega^2 r^2,$$
la ecuación de Schrödinger toma la forma
$$\left( \frac{d^2}{dr^2} + \frac{2m}{\hbar^2} \left( E_{n\ell} -\frac{1}{2} m\omega^2 r^2 - \frac{\hbar^2 \ell (\ell + 1)}{2mr^2} \right) \right) u_{n\ell} = 0.$$
Las soluciones son polinomios de Laguerre con valores propios dados por
$$E_{n\ell} = \hbar \omega \left( 2n + \ell -\frac{1}{2} \right),\ n=1,2,3,..\ y\ \ell=0,1,2,...\text{ para cualquier }n.$$
Si definimos $\Lambda=2n+\ell-2$, entonces los valores propios de la
energía
$$E_{n\ell} = \hbar \omega \left( \Lambda + \frac{3}{2} \right),\ con\ \Lambda = 0,1,2,...,$$
teniendo en cuenta que el estado base, para $\Lambda = 0$ no tienen
energía cero. Haciendo el mismo análisis del caso anterios, viendo las
degeneraciones y la cantidad de neutrones o protones que llenan cada
capa podemos saber como se cierra capa en este caso, pero cabe mencionar
que además de la degeneración en $m_{\ell}$ hay una degeneración extra
pues ciertas combinaciones de $n$ y $\ell$ dan el mismo valor de
$\Lambda$.
Las capas se cierran con
$$n= 2, 8, 20, 40, 70$$
De nueva cuenta tenemos unos pocos, pero no todos.
### Potencial espín-órbita {#potencial-espín-órbita .unnumbered}
En 1949 Maria Goeppert Mayer y Hans Jensen propusieron, para corregir
estos problemas, siguiendo el ejemplo del modelo atómico, que había un
fuerte acoplamiento espín-órbita responsable de esta diferencia
$$V_{TOT} = V(r)-f(r)\overrightarrow{L}\cdot \overrightarrow{S},$$
con los operadores de momento angular orbital y de espín, $f(r)$ es una
función arbitraria de la coordenada radial. En física atómica esta
interacción rompe la degenaración $j=\ell \pm \frac{1}{2}$ en dos
niveles, lo mismo sucede en física nuclear, aunque ahora con una función
de $r$.
El operador de momento angular
$$\begin{aligned}
\overrightarrow{J} =& \overrightarrow{L} + \overrightarrow{S} \\
\overrightarrow{J}^2 =& \overrightarrow{L}^2 + \overrightarrow{S}^2 + 2\overrightarrow{L} \cdot \overrightarrow{S} \\
\text{o despejando } \overrightarrow{L}\cdot \overrightarrow{S} =& \frac{1}{2}(\overrightarrow{J}^2 - \overrightarrow{L}^2 - \overrightarrow{S}^2),\end{aligned}$$
ambos operadores conmutan, por ello podemos definir así el cuadrado de
ambos operadores. Si definimos un estado por sus números cuánticos
$\ell$, $s$, $j$, $m_j$, nos quedamos con los primeros tres y obtenemos
$$\begin{aligned}
\langle \overrightarrow{L} \cdot \overrightarrow{S} \rangle &= \langle \frac{1}{2} (\overrightarrow{J}^2 - \overrightarrow{L}^2 - \overrightarrow{S}^2) \rangle \\
&= \frac{\hbar^2}{2} [j(j+1) - \ell(\ell + 1) - s(s+1)] \\
&= \frac{\hbar^2}{2} [j(j+1) - \ell(\ell + 1) - \frac{3}{4}] \\
&= \begin{cases}
\frac{\hbar^2}{2} \ell \quad &\text{para } j=\ell + \frac{1}{2} \\
-\frac{\hbar^2}{2}(\ell +1) \quad &\text{para } j=\ell - \frac{1}{2} \\
\end{cases}\end{aligned}$$
De aquí se obtienen los corrimientos en energía
$$\begin{aligned}
\Delta E_{n\ell}\left( j=\ell + \frac{1}{2} \right) =& -\frac{\hbar^2 \ell}{2} \int d^3r |\psi_{n\ell}(\overrightarrow{r})|^2 f(r) \\
\Delta E_{n\ell}\left( j=\ell - \frac{1}{2} \right) =& \frac{\hbar^2 (\ell+1)}{2} \int d^3r |\psi_{n\ell}(\overrightarrow{r})|^2 f(r)\end{aligned}$$
La diferencia entre estos dos corrimientos
$$\begin{aligned}
\Delta =& \Delta E_{n\ell}\left( j=\ell - \frac{1}{2} \right) - \Delta E_{n\ell}\left( j=\ell + \frac{1}{2} \right) \\
=& \hbar^2 \left( \ell + \frac{1}{2} \right) \int d^3r |\psi_{n\ell}(\overrightarrow{r})|^2 f(r)\end{aligned}$$
Para mayores valores de $\ell$ esta diferencia aumenta, de tal forma que
el nivel desdoblado se cruce con uno de energía menor, pero además
notemos que para una $j$ mayor el nivel se desdobla hacia abajo, como se
puede ver en la figura [6](#fig:shell){reference-type="ref"
reference="fig:shell"}.
 con licencia
[CC-BY-SA-3.0](https://creativecommons.org/licenses/by-sa/3.0)](shells.png){#fig:shell
width="0.5\\linewidth"}
Como en el modelo de Fermi debemos considerar los efectos de la barrera
de potencial coulombiano para protones, esto hace un desplazamiento en
los nivleles de energía, pero las características cualitativas no se ven
afectadas.
Ya vimos bastante del armado de este modelo, ahora ¿cuáles son su
logros? El más importante es que puede predecir de manera correcta el
espín y la paridad de un gran número de núcleos con $A$ impar. Como
hemos mencionado cada nivel se llena con un número par de protones o
neutrones, cada subcapa tienen dos protones o dos neutrones como máximo,
una con proyección del espín hacia arriba y otro con proyección hacia
abajo, hay un fuerte apareamiento y aportando cero al momento angular
total. Esto último está de acuerdo con los experimentos, los núcleos
par-par tienen momento angular total cero. Pero si hay un neutrón o
protón sin aparear, éste dará el valor de momento angular total del
núcleo, pero sólo uno, si hay un neutrón y un protón sin aparear el
modelo no puede decir nada de su espín.
Además nos puede dar la paridad de estos mismo núcleos, consideramos los
isóbaros ${}^{13}C^6$ y ${}^{13}Ni^7$ (núcleos espejo). Los $6$ protones
de ${}^13C^6$ y los 6 neutrones de ${}^13Ni^7$ están apareados, de esos
no nos ocupamos, lo que queremos ver es la configuración de los
neutrones en ${}^13C^6$ y la de los protones en ${}^13Ni^7$, de manera
análoga se acomodarán
$$(1S_{\frac{1}{2}})^2 (1P_{\frac{3}{2}})^4 (1P_{\frac{1}{2}})^1$$
El último nucleón no apareado cae en la capa $1P_{\frac{1}{2}}$,
entonces ambos núcleos tienen un espín de $\frac{1}{2}$ y una paridad de
$(-1)^{\ell=P=1}=-1$, entonces para ambos núcleos damos su paridad y
espín como $\frac{1}{2}^-$, que es el valor experimental.
Este modelo también es útil para calcular momentos magnéticos de los
núcleos. Sólo en núcleos pesados las predicciones no son buenas.
Modelo colectivo {#modelo-colectivo .unnumbered}
----------------
Las predicciones del modelo de capas fallan en núcleos pesados, no sólo
en espín y paridad pero sobre todo en momentos dipolares magnéticos, aún
para núcleos pesados con doble capa cerrada en los que parece que todo
ajusta de maravilla se tienen discrepancias en el momento cuadrupolar.
El problema como apunta esta última y significativa diferencia parece
radicar en la suposición de que el núcleo es esférico, mientras más
pesado menos lo es.
El modelo colectivo es de interacción fuerte, de manera análoga al
modelo de la gota. Propuesto por Aage Bohr, Ben Mottelson y James
Rainwater, las propiedades se asocian a un movimiento superficial de la
"gota" nuclear, las propiedades de núcleos pesados se podían obtener
suponiendo que la gota no tenía una forma esférica.
El modelo de capas funciona bastante bien ¿debemos desecharlo? No,
debemos encontrar un punto de contacto entre los modelos. El modelo de
la gota da más peso al movimiento colectivo de los nucleones, el modelo
de gas de Fermi y de capas piensa en partículas independientes. El punto
de conexión entre estos modelos está en el modelo colectivo, se
considera un núcleo de nucleones fuertemente ligado, y una capa con los
nucleones de valencia que se comportan como las moleculas superficiales
de una gota de agua. Este movimiento rompe la esfericidad del núcleo, se
puede ver como una perturbación que provoca que los nucleones de
valencia pasen de un estado sin perturbar en el modelo de capas a un
estado perturbado en el modelo colectivo.
El modelo colectivo puede pensarse como un modelo de capas pero con
potencial no esférico, esta no esfericidad rompe las simetrías
rotacionales, dando distintas propiedades y estados ante rotaciones y
vibraciones.
Consideramos el núcleo como un elipsoide
$$ax^2 + by^2 +\frac{z^2}{ab} = R^2$$
El potencial medio del movimiento nuclear
$$V(x,y,z)=\begin{cases}
0 \quad &\text{para } ax^2 + by^2 +\frac{z^2}{ab} \leq R^2 \\
\infty \quad &\text{de otra forma,} \\
\end{cases}$$
Como puede verse, los cálculos se volverán más complejos, no entraremos
en los detalles sólo nos quedaremos con las predicciones. Ahora se
agregan niveles de libertad rotacional y vibracional, tendremos un
momento rotacional $I$ asociado
10 Das, A., Ferbel, T. "Introduction to Nuclear and Particle Physics",
Segunda edición, World Scientific Publishing Co., 2003.
Henley, Ernest M., García, Alejandro "Subatomic Physics", Tercera
edición, World Scientific Publishing Co., 2007.